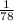Answer:
The maximum error is
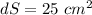
Relative error is Relative error is =
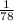
Explanation:
Circumference of a sphere C = 2
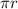
Differentiate above equation with respect to r
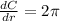
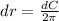
Given that
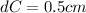

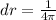
Surface area of the sphere S =
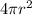
Differentiate above equation with respect to r
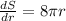
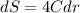
Where C = circumference of the sphere
given that C = 78 cm &
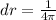
So the maximum error is given by
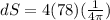
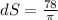
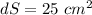
Now the relative error is given by
Relative error =
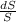
⇒
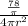
Since
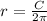
Relative error is =
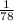
Therefore the maximum error is
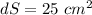
Relative error is Relative error is =