Question

In order to remove water from a flooded basement, two pumps, each rated at 40 gallons per minute, are used. After half an hour, the one pump burns out, and the second pump finishes removing the water half an hour later. How many gallons of water were removed from the basement?

Answer 1

3600 gallons of water was removed from the basement.

Explanation:

Given:

Rate of each pump = 40 gallons/min

We need to find find the number of gallons of water removed from the basement.

Solution:

Now Given:

After half an hour, the one pump burns out.

Now we know that;

1 hour = 60 mins

`\frac12` hour =
`(60)/(2)=30\ mins`

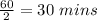
Now for 30 mins both the pumps were working and removing the water.

So we can say that;

Water remove for first 30 mins =
`40*2*30=2400\ gallons`

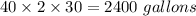
Also Given:

the second pump finishes removing the water half an hour later.

So we can say that;

Water removed for next 30 mins =
`40* 30*1 =1200\ gallons`

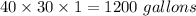
Now we can say that;

Total water removed from the basement is equal to sum of Water remove for first 30 mins and Water removed for next 30 mins .

framing in equation form we get;

Total water removed from the basement =
`2400+1200=3600\ gallons.`

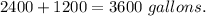
Hence 3600 gallons of water was removed from the basement.