Question

Help me please need help​

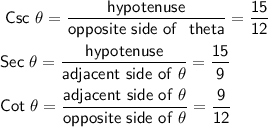
Answer 1

Explanation:

Hypotenuse: The longest side in the triangle and it is opposite to 90°

Opposite Side: The side oppoiste to the angle.

Adjacent side: The side next to the angle.

First find 'c' using Pythagorean theorem,

c² = 9² + 12²

= 81 + 144

= 225

c =√225

c = 15

`\sf \ Sin \ \theta = (opposite \ side \ of \ \theta)/(hypotenuse)= (12)/(15)`

`\sf \ Cos \ \theta = (adjacent \side \ of \ \theta)/(hypotenuse)= (9)/(15)\\\\ Tan \ \theta= (opposite \ side \ of \ \theta)/(adjacent \ side \ of \ \ theta)= (12)/(9)`

`\sf \ Csc \ \theta= (hypotenuse)/(opposite \ side \ of \ \ theta)= (15)/(12)\\\\\ Sec \ \theta = (hypotenuse)/(adjacent \ side \ of \ \theta)= (15)/(9)\\\\Cot \ \theta= (adjacent \ side \ of \ \theta)/(opposite \ side \ of \ \theta)= (9)/(12)`

`\sf \ Sin \ \alpha = (opposite \ side \ of \ \alpha \theta)/(hypotenuse)= (9)/(15)`

`\sf \ Cos \ \alpha = (adjacent \side \ of \ \alpha )/(hypotenuse)= (12)/(15)\\\\ Tan \ \alpha = (opposite \ side \ of \ \alpha )/(adjacent \ side \ of \ \ theta)= (9)/(12)`

`\sf \ Csc \ \alpha = (hypotenuse)/(opposite \ side \ of \ \alpha )= (15)/(9)\\\\\ Sec \ \alpha \theta = (hypotenuse)/(adjacent \ side \ of \ \alpha )= (15)/(12)\\\\Cot \ \alpha = (adjacent \ side \ of \ \alpha )/(opposite \ side \ of \ \alpha )= (12)/(9)`