Question

1. Find the kinetic energy of the uniform circular cone of height h, base radius R, and mass M. Rotating with the angular velocity ~ around an axis which goes through the center of mass. 2. The same for a uniform ellipsoid of semiaxes a, b, and c. 1 {

Answer 1

1) For the uniform circular cone, KE = 0.15MR²Ω²

2) For the ellipsoid, KE = 0.1M(a²+b²)Ω²

Step-by-step explanation:

1) For a circular cone rotating about the verical axis, the moment of inertia is given by
`I_(z) = (3)/(10) MR^(2)`

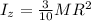
The kinetic energy of an object with angular velocity Ω is given by:

KE = 0.5 I Ω²

KE = o.5 * 0.3 MR²Ω²

KE = 0.15MR²Ω²

2) For a uniform ellipsoid of semi axes a, b, and c rotating in the vertical axis, the moment of inertia is given as
`I_(z) = (M)/(5) (a^(2) + b^(2) )`

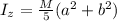
The kinetic energy is given by KE = 0.5 I Ω²

KE = o.5 * 0.2 M(a²+b²)Ω²

KE = 0.1M(a²+b²)Ω²

Answer 2

1)
`I = (3)/(10)\cdot m\cdot r^(2)`, 2)
`K = (1)/(10)\cdot m \cdot (b^(2)+c^(2))`

Step-by-step explanation:

1) The kinetic energy due to the rotation is:

`K = (1)/(2)\cdot I\cdot \omega^(2)`

Where
`I` and
`\omega` are the moment of inertia and angular speed, respectively. The moment of inertia of the circular cone is:

`I = (3)/(10)\cdot m\cdot r^(2)`

The kinetic energy is:

`K = (3)/(20)\cdot m\cdot r^(2)\cdot \omega^(2)`

2) The moment of inertia of the ellipsoid is (where a is the major semiaxis):

`I = (1)/(5)\cdot m \cdot (b^(2)+c^(2))`

The kinetic energy is:

`K = (1)/(10)\cdot m \cdot (b^(2)+c^(2))`