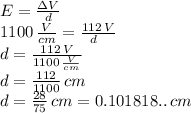Question

The electric field strength between the plates of a simple air Capacitor is equal to the voltage across the plates divided by the distance between them When a voltage of 112. V is put across the plates of such a capacitor an electric field strength of 1.1 kV/cm is measured.

Write an equation that will let you calculate the distance d between the plates.

Answer 1

`d=(112\,V)/(1100\,(V)/(cm)) \\d=(28)/(75) \,cm=0.101818.. \,cm`

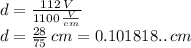
Step-by-step explanation:

Recall that the equation for the electric field intensity between the plates of a capacitor is given by:

`E=(\Delta V)/(d)`

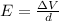
where E is the electric field,
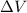`\Delta V` is the voltage across the plate of the capacitor, and "d" is the separation (distance) between the capacitor's plates.

So we need to solve for the distance in the equation above, but also make sure that the units for electric field and potential difference are in agreement. We then write the electric field strength in V/cm :

1.1kV/cm = 1100 V/cm

Now in the equation:

`E=(\Delta V)/(d)\\1100\,(V)/(cm) =(112\,V)/(d\\)\\d=(112\,V)/(1100\,(V)/(cm)) \\d=(112)/(1100) \,cm\\d=(28)/(75) \,cm=0.101818.. \,cm`