Answer:
The geometric sequence is
36,24,16,
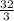 ,.......
,.......
Explanation:
The first term of the g.s is 36.
The 4th term of the given sequence is
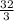 .
.
The
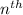 term of the geometric sequence is
term of the geometric sequence is

Where a is the first term of the geometric sequence and r is the geometric sequence.
Then 4th term of the sequence is
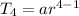
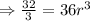
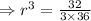
![\Rightarrow r=\sqrt[3]{ (8)/(27)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/o9gnk83l07eqmpmtps8223p1zfjg8sojph.png)
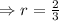
Then, second term of the sequence
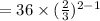

=24
The third term of the sequence is
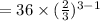
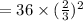
=16
The geometric sequence is
36,24,16,
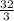 ,.......
,.......