Question

According to the local real estate board, the average number of days that homes stay on the market before selling is 78.4 with a standard deviation equal to 11 days. A prospective seller selected a random sample of 36 homes from the multiple listing service. Above what value for the sample mean should 95 percent of all possible sample means fall?a. About 64 days

b. About 79.3 days
c. Cannot be determined without knowing whether the population is normally distributed.
d. Approximately 75.4 days
e. 93.2 days

Answer 1

Correct option: (d) 75.4 days.

Explanation:

Let X = number of days that homes stay on the market before selling.

The average number of days that homes stay on the market before selling is, μ = 78.4 days.

The standard deviation of the number of days that homes stay on the market before selling is, σ = 11 days.

A sample of size, n = 36 homes are selected from the multiple listing service.

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sample mean will be approximately normally distributed.

Then the mean of the distribution of sample mean is given by,

`\mu_(\bar x)=\mu=78.4`

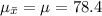
And the standard deviation of the distribution of sample mean is given by,

`\sigma_(\bar x)=(\sigma)/(√(n))=(11)/(√(36))=1.83`

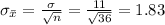
So, the distribution of sample mean is,
`\bar X\sim N(78.4,\ 1.83^(2))`.

Let
`\bar x` be the value of the sample mean above which 95% of all possible sample means fall.

That is,

`P(\bar X>\bar x)=0.95\\P(\bar X<\bar x)=0.05\\P(Z<z)=0.05`

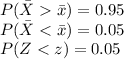
The value of z for the above probability is:

z = -1.645.

*Use a z-table for the value.

Compute the value of
`\bar x` as follows:

`z=(\bar x-\mu_(\bar x))/(\sigma_(\bar x))\\-1.645=(\bar x-78.4)/(1.83)\\\bar x=78.4-(1.645* 1.83)\\\bar x=75.389\\\bar x\approx75.4`

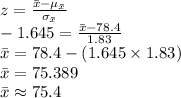
Thus, the sample mean above which 95% of all possible sample means fall is 75.4 days.