Question

2. Find the general relation of the equation cos3A+cos5A=0

Answer 1

`A=(\pi)/(8)+(n\pi)/(4)or\ A=(\pi)/(2)+n\pi`

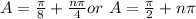
Explanation:

Find angles

`cos3A+cos5A=0`

________________________________________________________

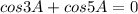
Transform the expression using the sum-to-product formula

`2cos((3A+5A)/(2))cos((3A-5A)/(2))=0`

________________________________________________________

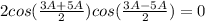
Combine like terms

`2cos((8A)/(2))cos((3A-5A)/(2))=0\\\\ 2cos((8A)/(2))cos((-2A)/(2))=0`

________________________________________________________

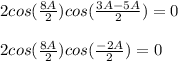
Divide both sides of the equation by the coefficient of variable

`cos((8A)/(2))cos((-2A)/(2))=0`

________________________________________________________

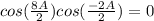
Apply zero product property that at least one factor is zero

`cos((8A)/(2))=0\ or\ cos((-2A)/(2))=0`

________________________________________________________

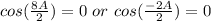
Cos (8A/2) = 0:

Cross out the common factor

`cos\ 4A=0`

________________________________________________________

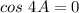
Solve the trigonometric equation to find a particular solution

`4A=(\pi)/(2)or\ 4A=(3\pi)/(2)`

________________________________________________________

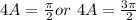
Solve the trigonometric equation to find a general solution

`4A=(\pi)/(2)+2n\pi \ or\\ \\ 4A=(3 \pi)/(2)+2n \pi\\ \\A=(\pi)/(8)+(n \pi)/(4\\)`

________________________________________________________

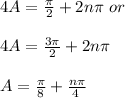
cos(-2A/2) = 0

Reduce the fraction

`cos(-A)=0`

________________________________________________________

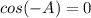
Simplify the expression using the symmetry of trigonometric function

`cosA=0`

________________________________________________________

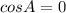
Solve the trigonometric equation to find a particular solution

`A=(\pi )/(2)\ or\ A=(3 \pi)/(2)`

________________________________________________________

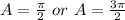
Solve the trigonometric equation to find a general solution

`A=(\pi)/(2)+2n\pi\ or\ A=(3\pi)/(2)+2n\pi,n\in\ Z`

________________________________________________________

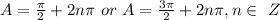
Find the union of solution sets

`A=(\pi)/(2)+n\pi`

________________________________________________________

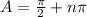
A = π/8 + nπ/4 or A = π/2 + nπ, n ∈ Z

Find the union of solution sets

`A=(\pi)/(8)+(n\pi)/(4)\ or\ A=(\pi)/(2)+n\pi ,n\in Z`

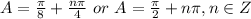
I hope this helps you

:)