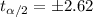Answer:
a) For the 90% confidence interval the value of
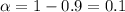 and
and
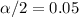 , with that value we can find the quantile required for the interval in the t distribution with df =3. And we can use the folloiwng excel code: "=T.INV(0.05,3)" and we got:
, with that value we can find the quantile required for the interval in the t distribution with df =3. And we can use the folloiwng excel code: "=T.INV(0.05,3)" and we got:
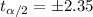
b) For the 99% confidence interval the value of
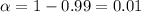 and
and
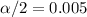 , with that value we can find the quantile required for the interval in the t distribution with df =106. And we can use the folloiwng excel code: "=T.INV(0.005,106)" and we got:
, with that value we can find the quantile required for the interval in the t distribution with df =106. And we can use the folloiwng excel code: "=T.INV(0.005,106)" and we got:
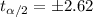
Step-by-step explanation:
Previous concepts
The t distribution (Student’s t-distribution) is a "probability distribution that is used to estimate population parameters when the sample size is small (n<30) or when the population variance is unknown".
The shape of the t distribution is determined by its degrees of freedom and when the degrees of freedom increase the t distirbution becomes a normal distribution approximately.
The degrees of freedom represent "the number of independent observations in a set of data. For example if we estimate a mean score from a single sample, the number of independent observations would be equal to the sample size minus one."
Solution to the problem
Part a
For the 90% confidence interval the value of
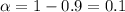 and
and
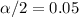 , with that value we can find the quantile required for the interval in the t distribution with df =3. And we can use the folloiwng excel code: "=T.INV(0.05,3)" and we got:
, with that value we can find the quantile required for the interval in the t distribution with df =3. And we can use the folloiwng excel code: "=T.INV(0.05,3)" and we got:
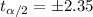
Part b
For the 99% confidence interval the value of
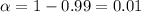 and
and
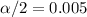 , with that value we can find the quantile required for the interval in the t distribution with df =106. And we can use the folloiwng excel code: "=T.INV(0.005,106)" and we got:
, with that value we can find the quantile required for the interval in the t distribution with df =106. And we can use the folloiwng excel code: "=T.INV(0.005,106)" and we got: