Question

A research institute poll asked respondents if they felt vulnerable to identity theft. In the poll, n=929 and x=523 who said "yes". Use a 99% confidence level.

a. Find the best point estimate of the population P. (Round to three decimal places as needed)
b. Identify the value of margin of error E. ________ (Round to four decimal places as needed)
c. Construct a confidence interval. ___ < p <. (Round to three decimal places as needed)
d. Write a statement that correctly interprets the confidence interval. Choose the correct answer bellow

1. One has 99% conficence that the interval from the lower bound to the upper boundactually does contain the true value of the population proportion.
2. 99% of sample proportions will fall between the lower bound and the upper bound.
3. there is a 99% chance that the true value of the population proportion will fall between the lower bound and the upper bound.
4. One has 99% confidence that the sample proportion is equal to the population proportion

Answer 1

Explanation:

Hello!

The variable of interest is

X: Number of people that feel vulnerable to identity theft in a sample of 929.

This variable is discrete and has a binomial distribution. X~Bi(n;p)

The parameter of interest is the population proportion of people that feel vulnerable to identity theft.

To calculate the 99% CI for the population proportion you have to use the approximate distribution to normal for the sample proportion p'≈N(p;
`(p(1-p))/(n)`)

a. The best point estimate for p is the sample proportion p' you calculate it as:

p'= x/n= 523/929= 0.56

b. The formula for the confidence interval is

p' ±
`Z_(1-\alpha /2) * \sqrt{(p'(1-p'))/(n) }`

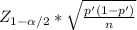
Where
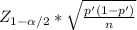`Z_(1-\alpha /2) * \sqrt{(p'(1-p'))/(n) }` is the margin of error

In this case
`Z_(1-\alpha /2)= Z_(0.995)= 2.586`

`Z_(1-\alpha /2) * \sqrt{(p'(1-p'))/(n) }= 2.586*\sqrt{(0.56*0.44)/(929) }= 0.04`

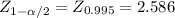
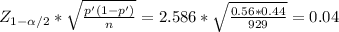
c. Then the interval is

0.56 ± 0.04

[0.52;0.6]

d.

With a 99% confidence level, you can expect that the interval [0.52;0.6] will include the true value of the proportion of people that feel vulnerable to identity theft.

The correct answer is

3. there is a 99% chance that the true value of the population proportion will fall between the lower bound and the upper bound.

I hope this helps!