Question

Select the three measurements that could be side lengths that form a right triangle

7cm
11cm
54 cm
60 cm
61 cm
65 cm

Answer 1

The side lengths of a right triangle is 11cm, 60cm and 61cm, that could be selected from the given measurements.

Explanation:

The measurements are,

7cm, 11cm, 54cm, 60cm, 61cm, 65cm

Step:1

To check the right angle triangle, Pythagorean theorem can be used.

For a Pythagorean theorem,

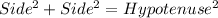`Side^(2) + Side^(2) = Hypotenuse^(2)`..........................(1)

The side values are lower than the hypotenuse,

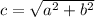`c=\sqrt{a^(2)+b^(2) }`...................................(2)

Where,

a,b - side values

c - Hypotenuse

For right angle triangle, c > a, b

Alternative : 1

Take, a = 7cm, b = 11cm

From eqn (2),

`c = \sqrt{7^(2)+11^(2) }` =
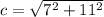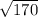`√(170)` = 13.04

The above value is not equal to the any one of the values of ( 54cm. 60cm, 61cm, 65cm ), So its not an sides of right triangle.

Alternative : 2

Take, a = 7cm, b = 54cm

From eqn (2),

`c = \sqrt{7^(2)+54^(2) }` =
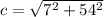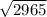`√(2965)` = 54.45

The above value is not equal to the any one of the values of (60cm, 61cm, 65cm ), So its not an sides of right triangle.

Alternative : 3

Take, a = 7cm, b = 60cm

From eqn (2),

`c = \sqrt{7^(2)+60^(2) }` =
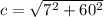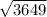`√(3649)` = 60.406

The above value is not equal to the any one of the values of (61cm, 65cm ), So its not an sides of right triangle.

Alternative : 4

Take, a = 7cm, b = 61cm

From eqn (2),

`c = \sqrt{7^(2)+61^(2) }` =
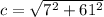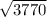`√(3770)` = 61.40

The above value is not equal to the values of (65cm ), So its not an sides of right triangle.

Alternative : 5

Take, a = 11cm, b = 54cm

From eqn (2),

`c = \sqrt{11^(2)+54^(2) }` =
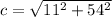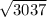`√(3037)` = 55.1089

The above value is not equal to the any one of the values of (60cm, 61cm, 65cm ), So its not an sides of right triangle.

Alternative : 6

Take, a = 11cm, b = 60cm

From eqn (2),

`c = \sqrt{11^(2)+60^(2) }` =
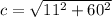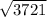`√(3721)` = 61

The above value is equal to the values of (61cm ), So its an sides of right triangle. The three sides are 11, 60 and 61.

Step:2

Check for solution,

`11^(2) + 60^(2) = 61^(2)`

`3721=3721`

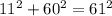
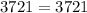
Result:

The side lengths of a right triangle is 11cm, 60cm and 61cm, that could be selected from the given measurements.