Question

Can someone help me find the area to this pentagon??

Answer 1

990.9

Explanation:

A=1/45(5+25)a2=1/4·5·(5+2·5)·242≈990.99498

*bold is where a square root is

Answer 2

Area =
`991\, cm^2`

Explanation:

Recall that the area of any regular polygon is expressed via the formula:

Area = perimeter * apothem /2

The perimeter is easy to find since in our case it would be 24 cm * 5 (five sides of the same 24 cm length). Perimeter = 120 cm

In order to find the dimension of the apothem (which is pictured as an orange segment in the attached image) we use the fact that the apothem joins the center of the polygon at the exact middle of each side (thus rendering two 12 cm segments), and forming a 90 degree angle. Seeing from the picture, we can use the information on the small right angle triangles that are formed by the apothem and the sides of the triangles drawn joining the center of the polygon with its vertices.

Recall that the five equal angles around the center point, have to measure 360 degrees / 5 = 72 degrees, so, half of this (which is one of the acute angles of the small right angle triangles we are going to use to find the apothem) has to be 36 degrees.

We can then use the definition of tangent of one of the acute angles in a right angle triangle:

the tangent of the angle (36 degrees) equals the quotient of the side opposite to it (12 cm) divided by the adjacent side (apothem). Using this relationship we can solve for the apothem:

`tan(36^o)=(12\,cm)/(apothem) \\apothem=(12)/(tan(36^o)) cm\\apothem =16.516583\, cm`

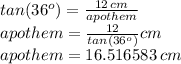
Now we can find the area using the area formula above:

Area = perimeter * apothem / 2

Area = 120 cm * 16.516583 cm / 2

Area = 990.99 cm^2

which we can round to approximately 991 square cm