Answer: x
In other words, the input variable
If f(x) is some function and g(x) is its inverse, then these two properties are always true for every x value in the domain of f(x) and g(x)
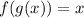

An example:
Let f(x) = x/3, then g(x) = 3x. The f(x) function takes the input and divides by 3, while the g(x) inverse function does the opposite and multiplies inputs by 3. The two opposite operations cancel out to leave the original input. If you were to say plug in x = 27, then f(27) = 9 which is then plugged into g(x) to get g(9) = 27. Therefore, g( f(27) ) = g( 9 ) = 27. The same idea works in reverse too.