Question

Given: Lateral area = 68

AO = 3.4

Find: m∠SAB

Answer 1

`\alpha=57.72^o`

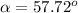
Explanation:

Surface Area of a Cone

The surface area of a cone is given by

`S=\pi r.h_s`

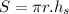
Where r is the radius and hs is the slant height measured from the top to any point at the circumference of the base. The cone shown in the figure has a radius r=3.4 and a surface area of 68.

Solving for hs

`\displaystyle h_s=(S)/(\pi . r)`

`\displaystyle h_s=(68)/(\pi \cdot 3.4)`

`h_s=6.37`

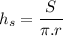
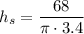
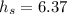
But hs is equal to AS. The triangle SAO has an angle of 90° at the point O. The required angle m∠SAB can be found by applying the cosine ratio:

`\displaystyle cos\alpha=(AO)/(AS)=(3.4)/(6.37)=0.53`

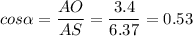
Thus

`\boxed{\alpha=57.72^o}`