Question

PLEASE HELP ASAP

Write the absolute value equations in the form

|x−b|=c (where b is a number and c can be either number or an expression) that have the following solution sets:

All numbers such that x≤5.

Answer 1

|x-5|=(-x+5)

你们好你们好你们好你们好

Answer 2

Explanation:

The problem asks to find the values "b" and "c" in a way that

the solutions of the equation |x - b| = c are x= 1/2 and x= -1/3.

It means that "b" is the center of the segment [-
`(1)/(3) ,(1)/(2)`].

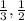This segment has the length
`(1)/(2) - ( - (1)/(3) = (1)/(2) + (1)/(3) = (3)/(6) + (2)/(6) = (5)/(6)` Hence, the half of this length is
`(5)/(12)`.

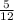Therefore, the center of the segment is
`(1)/(2) - (5)/(12) = (6)/(12) - (5)/(12) = (1)/(12)`

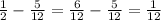
Thus the value of "b" is found: it is b =
`(1)/(12)`.

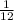Then the value of "c" is c =
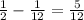`(1)/(2) - (1)/(12) = (5)/(12)`.