Question

A car driving at 20m/s accelerates at 3m/s2 for 3s. What is its final velocity? How far will it travel during this time?

Answer 1

Answers:

Final velocity = 29 m/s

Distance traveled = 73.5 meters

========================================================

Work Shown:

The given data is

`v_i = 20 \text{ m}/\text{s} = \text{initial velocity}\\\\a = 3 \text{ m}/\text{s}^2 = \text{acceleration}\\\\t = 3 \text{ s} = \text{time duration}\\\\`

This leads to

`v_f = v_i + a*t\\\\v_f = 20 + 3*3\\\\v_f = 20 + 9\\\\v_f = 29\\\\`

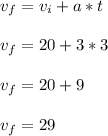
The final velocity is 29 m/s.

----------

We can use that final velocity to find the distance traveled.

`x = 0.5*(v_i+v_f)*t\\\\x = 0.5*(20+29)*3\\\\x = 0.5*(49)*3\\\\x = 24.5*3\\\\x = 73.5\\\\`

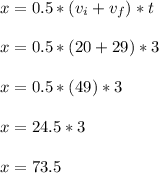
The distance traveled is 73.5 meters.

----------

An alternative way to calculate the distance is to do this

`x = ((v_f)^2 - (v_i)^2)/(2a)\\\\x = ((29)^2 - (20)^2)/(2*3)\\\\x = (841 - 400)/(6)\\\\x = (441)/(6)\\\\x = 73.5\\\\`

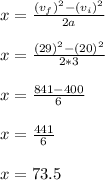
Or you could do this

`x = v_i*t + 0.5*a*t^2\\\\x = 20*3 + 0.5*3*3^2\\\\x = 20*3 + 0.5*3*9\\\\x = 60 + 13.5\\\\x = 73.5\\\\`

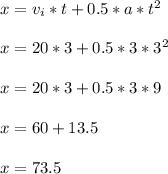
For more information, check out the Kinematics equations.