Answer:
The population after 50 years will be 1850.
Explanation:
We are given the following in the question:

which is the recursive rule for a population.
Initial population = 100
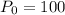
The explicit form of given recursive relation can be written as:
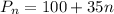
We have to find the population after 50 years.
We put n = 50 in the explicit form.

Thus, the population after 50 years will be 1850.