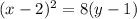Question

Find the equation of the parabola with focus (2, 3) and directrix y = -1. A) (y - 1)2 = 8(x - 2) B) (y - 1)2 = 4(x - 2) C) (x - 2)2 = 8(y - 1) D) (x - 2)2 = 4(y - 1)

Answer 1

The correct option is option (C).

The required equation of the parabola is

`(x-2)^2=8(y-1)`

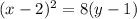
Explanation:

Formula:

• The distance of a point (x₁,y₁) from a line ax+by+c=0 is

`(ax_1+by_1+c)/(√(a^2+b^2))`.

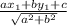• The distance between two points (x₁,y₁) and (x₂,y₂) is
  `√((x_2-x_1)^2+(y_2-y_1)^2)`

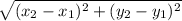
Given that, the focus of the parabola is (2,3) and directrix y= - 1.

We know that, a parabola is the locus of points that equidistant from the directrix and the focus.

Let any point on the parabola be P(x,y) .

The distance of P from the directrix is

`=\frac{y+1}{\sqrt {1^2}}`

=y+1

The distance of the point P from the focus (2,3) is

`√((x-2)^2+(y-3)^2)`

According to the problem,

`√((x-2)^2+(y-3)^2)=y+1`

`\Rightarrow (x-2)^2+(y-3)^2=(y+1)^2`

`\Rightarrow (x-2)^2+y^2-6y+9=y^2+2y+1`

`\Rightarrow (x-2)^2=y^2+2y+1-y^2+6y-9`

`\Rightarrow (x-2)^2=8y-8`

`\Rightarrow (x-2)^2=8(y-1)`

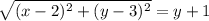
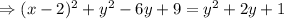
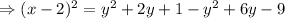
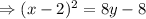
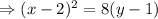
The required equation of the parabola is

`(x-2)^2=8(y-1)`