Question

Find the vertices and foci of the hyperbola with equation.

quantity x minus 3 squared divided by 81 minus the quantity of y plus 5 squared divided by 144 equals 1

Vertices: (-5, 15), (-5, -9); Foci: (-5, -9), (-5, 15)
Vertices: (12, -5), (-6, -5); Foci: (-12, -5), (18, -5)
Vertices: (-5, 12), (-5, -6); Foci: (-5, -12), (-5, 18)
Vertices: (15, -5), (-9, -5); Foci: (-9, -5), (15, -5)

Answer 1

The vertices are (12 , -5) , (-6 , -5)

The foci are (18 , -5) and (-12 , -5) ⇒ 2nd answer

Explanation:

The standard form of the equation of a hyperbola with center (h , k) and transverse axis parallel to the x-axis is
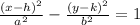`((x-h)^(2))/(a^(2))-((y-k)^(2))/(b^(2))=1` , where

• The coordinates of the vertices are (h ± a , k)

• The coordinates of the foci are (h ± c , k), where c² = a² + b²

∵ The equation of the hyperbola is
`((x-3)^(2))/(81)-((y+5)^(2))/(144)=1`

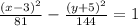
- Compare it with the form above

∴ h = 3 and k = -5

∴ a² = 81

- Take √ for both sides

∴ a = ± 9

∴ b² = 144

- Take √ for both sides

∴ b = ± 12

∵ Its vertices are (h + a , k) and (h - a , k)

∵ h + a = 3 + 9 = 12

∵ h - a = 3 - 9 = -6

∵ k = -5

∴ Its vertices are (12 , -5) , (-6 , -5)

∵ c² = a² + b²

∴ c² = 81 + 144

∴ c² = 225

- take √ for both sides

∴ c = ± 15

∵ Its foci are (h + c , k) and (h - c , k)

∵ h + c = 3 + 15 = 18

∵ h - c = 3 - 15 = -12

∵ k = -5

∴ Its foci are (18 , -5) and (-12 , -5)