Question

Find the center, vertices, and foci of the ellipse with equation 2x2 + 7y2 = 14.

Center: (0, 0); Vertices: (-7, 0), (7, 0); Foci: Ordered pair negative 3 square root 5 comma 0 and ordered pair 3 square root 5 comma 0
Center: (0, 0); Vertices: Ordered pair negative square root 7 comma 0 and ordered pair square root 7 comma 0; Foci: Ordered pair negative square root 5 comma 0 and ordered pair square root 5 comma 0
Center: (0, 0); Vertices: Ordered pair 0 comma negative square root 7 and ordered pair 0 comma square root 7; Foci: Ordered pair 0 comma negative square root 5 and ordered pair 0 comma square root 5
Center: (0, 0); Vertices: (0, -7), (0, 7); Foci:Ordered pair 0 comma negative 3 square root 5 and ordered pair 0 comma 3 square root 5

Answer 1

Center: (0 , 0); Vertices: (
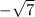`-√(7)` , 0) and (
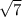`√(7)` , 0); Foci: (
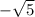`-√(5)` , 0) and (
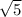`√(5)` , 0) ⇒ 2nd answer

Explanation:

The standard form of the equation of an ellipse with center (0 , 0 ) and major axis parallel to the x-axis is
`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` , a > b , where

• The coordinates of the vertices are (± a , 0)
• The coordinates of the foci are (± c , 0), and c ² = a² - b²

∵ The equation of the ellipse is 2x² + 7y² = 14

- Divide both sides by 14 to make the right hand side = 1

∴
`(2x^(2))/(14)+(7y^(2))/(14)=(14)/(14)`

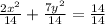
- Simplify the fractions

∴
`(x^(2))/(7)+(y^(2))/(2)=1`

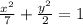
Compare it with the form of the ellipse above

∴ The center of the ellipse is (0 , 0)

∴ a² = 7

- Take √ for both sides

∴ a = ±
`√(7)`

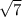
∴ b² = 2

- Take √ for both sides

∴ b = ±
`√(2)`

∵ The vertices of it are (a , 0) and (-a , 0)

∴ Its vertices are (
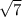`√(7)` , 0) and (
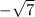`-√(7)` , 0)

∵ c² = a² - b²

∵ a² = 7 and b² = 2

∴ c² = 7 - 2

∴ c² = 5

- Take √ for both sides

∴ c = ±
`√(5)`

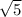
∵ The foci of it are (c , 0) and (-c , 0)

∴ Its foci are (
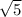`√(5)` , 0) and (
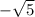`-√(5)` , 0)