Question

Working together, it takes 2 computers 12 minutes to send out emails. If it takes the slower 30 minutes to the job on its own, how long it take the fast computers to do the job on its own

Answer 1

The faster computer can do the job in 20 mins on it own.

Explanation:

Given:

Time taken by slower computer to do job on its own =30 minutes.

Time taken by both the computers to do the job = 12 mins.

We need to find the Time taken by faster computer to do job on its own.

Solution:

Let the the Time taken by faster computer to do job on its own be 'x'.

Now we know that;

Rate to complete the job is equal to number of jobs divided by time taken to complete the job.

Rate of faster computer =
`\frac1x`

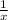
Rate of slower computer =
`(1)/(30)`

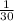
Rate of both the computers =
`(1)/(12)`

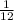
Now we can say that;

Rate of both the computers is equal to sum of Rate of faster computer and Rate of slower computer.

framing in equation form we get;

`(1)/(12)=(1)/(30)+(1)/(x)\\\\(1)/(x) = (1)/(12)-(1)/(30)`

Now we will take the LCM to make the denominator common we get;

`(1)/(x)=(5)/(12*5)-(2)/(30*2)\\\\\frac1x=(5)/(60)-(2)/(60)`

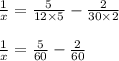
Now denominator are same so we will solve the numerator.

`\frac1x=(5-2)/(60)\\\\\frac1x=(3)/(60)\\\\\frac1x=(1)/(20)\\\\x=20\ mins`

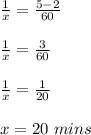
Hence The faster computer can do the job in 20 mins on it own.