Question

1. Find the average rate of change of the function, f(x) = log2 (4x) on the interval of x = 2 to x = 8

Answer 1

Given:

It is given that the function is
`f(x)=\log _(2)(4 x)`

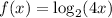
We need to determine the average rate of change of the function over the interval x = 2 to x = 8.

Value of f(2):

Substituting x = 2 in the function, we get;

`f(2)=\log _(2)(4 (2))`

`f(2)=\log _(2)(8)`

`f(2)=3`

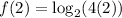
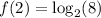
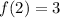
Thus, the value of f(2) is 3.

Value of f(8):

Substituting x = 8 in the function, we get;

`f(8)=\log _(2)(4 (8))`

`f(8)=\log _(2)(32)`

`f(8)=5`

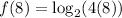
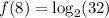
Thus, the value of f(8) is 5.

Average rate of change:

The average rate of change can be determined using the formula,

`Average=(f(b)-f(a))/(b-a)`

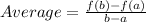
Substituting a = 2 and b = 8 in the above formula, we get;

`Average=(f(8)-f(2))/(8-2)`

`Average=(5-3)/(8-2)`

`Average=(2)/(6)`

`Average=(1)/(3)`

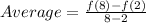
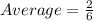
Thus, the average rate of change over the interval x = 2 to x = 8 is
`(1)/(3)`