Question

A baseball is thrown with an upward velocity of 32 feet per second. The equation h=-16t^2+32t gives the height of the ball t seconds after it's thrown. Determine whether the function has a maximum or minimum value.

Answer 1

The function of height has a maximum value.

Explanation:

Maximum or Minimum:

A given function f(x).

1. Find out f'(x) and f''(x)
2. Then set f'(x)=0 which gives x=a.
3. f''(a) > 0 , then at x=a , f(x) has minimum value.
4. If f''(a)<0 , then at x=a, f(x) has maximum value.

Given that, a baseball is thrown with with an velocity of 32 feet per second.

The equation of height is

`h=-16t^2+32t`

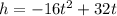
Differentiating with respect to t

`h'=-32 t+32`

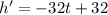
Again differentiating with respect to t

`h''=-32`

Next, we set h'=0

`-32 t+32=0`

`\Rightarrow 32t=32`

`\Rightarrow t=1`

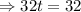
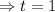
Now
`h''|_(t=1)=-32<0`

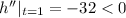
Since at t=1, h''<0.

The function of height has a maximum value.

The maximum of h is = -16.(1)²+32

= -16+32

=16 feet