Question

Here are the scores that Jenna has received on her

seven quizzes:
16, 13, 20, 16, 12, 17, 18
What is the variance rounded to the nearest tenth?
Enter

Answer 1

Given:

The scores that Jenna has received on her seven quizzes is 16, 13, 20, 16, 12, 17, 18.

We need to determine the variance.

Mean:

The mean of the data is given by

`Mean=(16+13+20+16+12+17+18)/(7)`

`Mean=(112)/(7)`

`Mean=16`

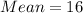
Thus, the mean of the given data is 16.

Variance:

The variance of the data can be determined using the formula,

`variance =(\sum(X-\mu)^(2))/(n)`

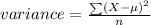
where
`\mu` is the mean and n is the number of terms in the distribution.

Thus, we have;

`variance=((16-16)^2+(13-16)^2+(20-16)^2+(16-16)^2+(12-16)^2+(17-16)^2+(18-16)^2)/(7)`

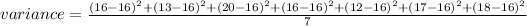
Simplifying the terms, we get;

`variance=((0)^2+(-3)^2+(4)^2+(0)^2+(4)^2+(1)^2+(2)^2)/(7)`

`variance=(0+9+16+0+16+1+4)/(7)`

`variance=(46)/(7)`

`variance=6.57`

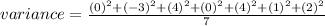
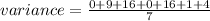
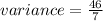
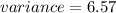
Rounding off to the nearest tenth, we get;

`variance=6.6`

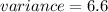
Thus, the variance is 6.6