Answer:
Proved down
Explanation:
To prove that a triangle is isosceles use the distance formula to find the length of its side and check if there are two sides equal.
To prove that a triangle is right find the square of the longest side and then find the sum of the squares of the other two sides, if the two answers are equal, then the triangle is right (converse of Pythagoras Theorem).
The formula of the distance between two points is:
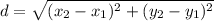
∵ x = (-1 , 5) and y = (4 , 4)
∴
 = -1 and
= -1 and
 = 4
= 4
∴
 = 5 and
= 5 and
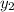 = 4
= 4
- Substitute them in the formula of the distance to find xy
∵
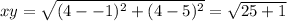
∴
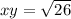
∵ x = (-1 , 5) and z = (-2 , 0)
∴
 = -1 and
= -1 and
 = -2
= -2
∴
 = 5 and
= 5 and
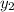 = 0
= 0
- Substitute them in the formula of the distance to find xz
∵
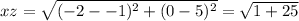
∴
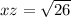
∵ xy = xz
- The isosceles triangle has two equal sides
∴ Δ xyz is an isosceles triangle
∵ y = (4 , 4) and z = (-2 , 0)
∴
 = 4 and
= 4 and
 = -2
= -2
∴
 = 4 and
= 4 and
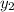 = 0
= 0
- Substitute them in the formula of the distance to find yz
∵
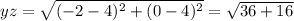
∴
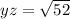
yz is the longest side lets find its square
∵ (yz)² = (
 )²
)²
∴ (yz)² = 52
- Lets find the sum of the squares of the other two sides
∵ (xy)² + (xz)² = (
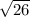 )² + (
)² + (
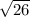 )²
)²
∴ (xy)² + (xz)² = 26 + 26 = 52
∴ (yz)² = (xy)² + (xz)²
- That means the angle opposite to yz is a right angle
∴ Δ xyz is a right isosceles triangle