Answer:
The mean is 4.5 and the standard deviation is 1.44.
Explanation:
An uniform probability is a case of probability in which each outcome is equally as likely.
For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.
The mean of the uniform probability distribution is:
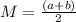
The standard deviation of the uniform probability distribution is:
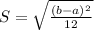
Uniformly distributed random variable ranging from 2 to 7.
This means that
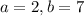 .
.
So
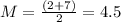
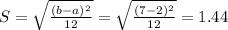
The mean is 4.5 and the standard deviation is 1.44.