Answer:
The value of Rebecca's investment equals the value of Hector's investment after approximately 15.8 years to the nearest tenth
The common value of the investments is approximately $2358.05
Explanation:
The formula of the compound interest including the principal is
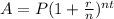 , where
, where
- A is the future value of the investment/loan, including interest
- P is the principal investment amount
- r is the annual interest rate (decimal)
- n is the number of times that interest is compounded per unit t
- t is the time the money is invested or borrowed for
Hector invests $800 in an account that earns 6.96% annual interest compounded semiannually
∵ P = 800
∵ r = 6.96 =
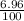 = 0.0696
= 0.0696
∵ n = 2 ⇒ semiannually
- Substitute all these values in the formula to find future value
∴

∴
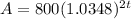
Rebecca invests $1,000 in an account that earns 5.44% annual interest compounded monthly
∵ P = 1,000
∵ r = 5.44 =
 = 0.0544
= 0.0544
∵ n = 12 ⇒ monthly
- Substitute all these values in the formula to find future value
∴
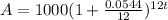
∴
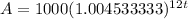
∵ Rebecca's investment equals the value of Hector's investment
- Equate the two equations
∵
 =
=
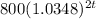
- Insert ㏑ in both sides and remember ㏑(ab) = ㏑(a) + ㏑(b)
∴ ㏑(
 ) = ㏑(
) = ㏑(
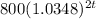 )
)
∴ ㏑(1000) + ㏑(
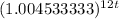 ) = ㏑(800) + ㏑(
) = ㏑(800) + ㏑(
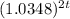 )
)
- Remember
 = n ㏑(a)
= n ㏑(a)
∴ ㏑(1000) + 12t [㏑(1.004533333)] = ㏑(800) + 2t [㏑(1.0348)]
- Subtract ㏑(800) and 12t [㏑(1.004533333)] from both sides
∴ ㏑(1000) - ㏑(800) = 2t [㏑(1.0348)] - 12t [㏑(1.004533333)]
- Take t as a common factor from the right hand side
∴ ㏑(1000) - ㏑(800) = t(2[㏑(1.0348)] - 12[㏑(1.004533333)])
- Divide both sides by (2[㏑(1.0348)] - 12[㏑(1.004533333)])
∴ 15.8 = t
The value of Rebecca's investment equals the value of Hector's investment after approximately 15.8 years to the nearest tenth
Let us find this value using Hector or Rebecca equations
∵
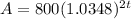
- Substitute t by 15.8
∴
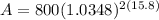
∴ A = 2358.05
The common value of the investments is approximately $2358.05