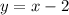Answer:
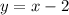
Explanation:
So we are given the formula for the slope of a hyperbola in this form:
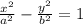 .
.
That formula for the slope is
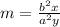
If we compare the following two equations, we will be able to find
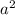 and
and
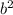 :
:
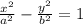
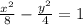
We see that
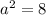 while
while
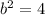 .
.
So the slope at
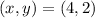 is:
is:
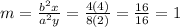 .
.
Recall: Slope-intercept form of a linear equation is
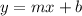 .
.
We just found
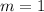 . Let's plug that in.
. Let's plug that in.
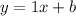
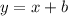
To find
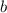 , the
, the
 -intercept, we will need to use a point on our tangent line. We know that it is going through
-intercept, we will need to use a point on our tangent line. We know that it is going through
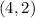 .
.
Let's enter this point in to find
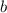 .
.
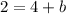
Subtract 4 on both sides:
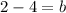
Simplify:
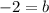
The equation for the tangent line at
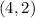 on the given equation is:
on the given equation is: