Question

A random sample of 28 plastic items is obtained, and their breaking strengths are measured. The sample mean is 7.142 and the sample standard deviation is 0.672. Conduct a hypothesis test to assess whether there is evidence that the average breaking strength is not 7.000.

Answer 1

The test statistic t = 1.126 < 1.703 of '27' degrees of freedom at 0.05 level of significance.

null hypothesis(H₀ ) is accepted

There is evidence that the average breaking strength is 7.000.

Explanation:

Step 1:-

Given random sample size (n) =28 <30

small sample size n= 28

The sample mean (x⁻) = 7.142

sample standard deviation (S) =0.672

Step 2:-

Null hypothesis :- there is evidence that the average breaking strength is 7.000.

H₀ : μ =7

Alternative hypothesis:-there is evidence that the average breaking strength is 7.000.

H₁ : μ ≠7

The test statistic
`t = (x^(-) -mean)/((S)/(√(n) ) )`

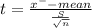
Substitute all values and simplification ,

`t = (7.142 -7)/((0.672)/(√(28) ) ) = (0.142 )/(0.1269)`

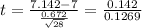
t = 1.126

Calculated value is t = 1.126

The degrees of freedom γ = n-1 = 28-1 =27

The tabulated value t= 1.703 at degrees of freedom at 0.05 level of significance.

since calculated t < tabulated value 't' value of 27 degrees of freedom at 0.05 level of significance.

null hypothesis(H₀ ) is accepted

There is evidence that the average breaking strength is 7.000.