Consider a circle with radius
 centered at some point
centered at some point
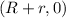 on the
on the
 -axis. This circle has equation
-axis. This circle has equation
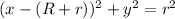
Revolve the region bounded by this circle across the
 -axis to get a torus. Using the shell method, the volume of the resulting torus is
-axis to get a torus. Using the shell method, the volume of the resulting torus is
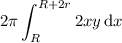
where
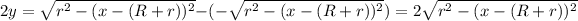 .
.
So the volume is
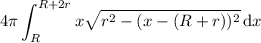
Substitute
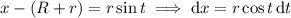
and the integral becomes
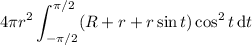
Notice that
 is an odd function, so the integral over
is an odd function, so the integral over
![\left[-\frac\pi2,\frac\pi2\right]](https://img.qammunity.org/2021/formulas/mathematics/college/3tzvbt8kvxceuwbzhen04z08n1862b8ckn.png) is 0. This leaves us with
is 0. This leaves us with
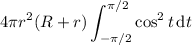
Write
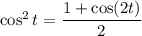
so the volume is
