Question

An automobile tire having a temperature of 3.4 ◦C (a cold tire on a cold day) is filled to a gauge pressure of 24 lb/in2 . What would be the gauge pressure in the tire when its temperature rises to 26◦C? For simplicity, assume that the volume of the tire remains constant, that the air does not leak out and that the atmospheric pressure remains constant at 14.7 lb/in2 . Answer in units of lb/in2 .

Answer 1

27.16 lb/in²

Step-by-step explanation:

initial temperature, T1 = 3.4 °C = 276.4 K

initial gauge pressure, P1 = 24 lb/in²

atmospheric pressure, Po = 14.7 lb/in²

initial absolute pressure, P1' = Po + P1 = 14.7 + 24 = 38.7 lb/in²

final temperature, T2 = 26 °C = 299 K

Let the final gauge pressure is P2.

use the ideal gas equation and the volume is constant.

`(P_(1)')/(T_(1))=(P_(2)')/(T_(2))`

`(38.7)/(276.4)=(P_(2)')/(299)`

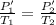
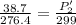
P2' = 41.86 lb/in²

Now the gauge pressure, P2 = P2' - Po = 41.86 - 14.7 = 27.16 lb/in²

Thus, the new gauge pressure is 27.16 lb/in².

Answer 2

`27.164 lb/in^2`

Step-by-step explanation:

We are given that

Gauge pressure at 3.4 degree Celsius,P=
`24lb/in^2`

We have to find the gauge pressure in tire when the temperature rises to 26 degree Celsius.

Atmospheric pressure=
`14.7lb/in^2`

`P_1=P+14.7=24+14.7=38.7lb/in^2`

K=273+Degree Celsius

`T_1=3.4+273=276.4 K`

`T_2=26+273=299K`

`P_2=(P_1T_2)/(T_1)`

`P_2=(38.7* 299)/(276.4)`

`P_2=41.864 lb/in^2`

Gauge pressure in tire when the temperature rises to 26 degree Celsius.=
`41.864-14.7=27.164lb/in^2`