Answer:
The magnetic field that is necessary is equal to 1.88x10⁻⁴ T
Step-by-step explanation:
If the electron is accelerated:
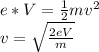
Where
e = 1.6x10⁻¹⁹C
V = 2.8 kV = 2800 V
m = 9.1x10⁻³¹kg
Replacing:

When the electron is moving in straight line, the magnetic force is balanced with the electric force, thus:
V = E * d
Where V = 100 V
d = 17 mm = 0.017 m
E = V/d = 100/0.017 = 5882.35 N/C
The magnetic field that is necessary is equal to:
B = E/v = 5882.35/3.13x10⁷ = 1.88x10⁻⁴ T