Answer:
We are 99% confident interval for the population proportion of passing test scores between ( 0.5987 and 0.9413 )
Explanation:
Given -
n = 40
Population proportion =
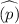 =
=
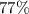 = .77
= .77
1 -
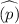 = 1 - .77 =.23
= 1 - .77 =.23
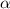 = 1 - confidence interval = 1 - .99 = .01
= 1 - confidence interval = 1 - .99 = .01
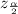 =
=
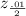 = 2.58
= 2.58
99% confidence interval for the population proportion of passing test scores=
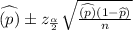
=
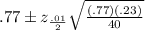
=
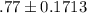
=
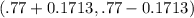
= ( 0.5987 , 0.9413 )