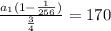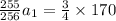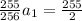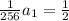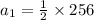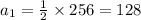Answer:
The first term is 128
Explanation:
The common ratio of the geometric series is given as:
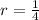
The sum of the first 4 term is 170.
The sum of first n terms of a geometric sequence is given b;
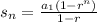
We put the common ratio, n=4 and equate to 170.
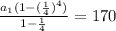
Simplify: