Question

Knowing that the horizontal distance between points A and G as well as G and B is 25 cm and knowing that the maximum width of the of the racket head is 30 cm, determine the velocity of Points A and B.

Answer 1

Complete Question:

A tennis racket is thrown vertically into the air. The center of gravity G has a velocity of 5 m/s upwards. Angular velocity about the x - direction of 1 rad/s and angular velocity about the y - direction of 20 rad/s. Knowing that the horizontal distance between points A and G as well as G and B is 25 cm and knowing that the maximum width of the of the racket head is 30 cm, determine the velocity of Points A and B.

Answer:

a)
`v_(A) = 10 m/s`

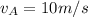
b)

`v_(B) = 3i + 0.15 j m/s\\v_(B) = \sqrt{3^(2) + 0.15^(2) }\\v_(B) = 3.004 m/s`

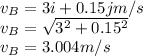
Step-by-step explanation:

a) Velocity of point A

The velocity of point A is a combination of the translational and the rotational velocity of the racket.

`v_(A) = v_(G) + v_(r)`

`v_(G) = 5 m/s`

`v_(r) = wr`

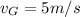
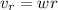
r = 25 cm = 0.25 m

w = 20 rad/s

`v_(r) = 20 * 0.25\\v_(r) = 5 m/s`

`v_(A) = 5 + 5\\v_(A) = 10 m/s`

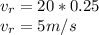
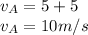
b) Velocity of point B

At point B, the linear velocity is in the +ve z-direction while the rotational velocity is in the -ve z-direction:

`v_(G) = 5 m/s`

`v_(r) = -r w\\v_(r) = - 0.25 * 20\\v_(r) = - 5 m/s`

`v_(Bz) = v_(G) + v_(r) \\v_(Bz) = 5 -5\\v_(Bz) = 0 m/s`

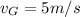
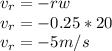
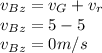
In the y - direction, r = 30/2 = 15 cm = 0.15 m

r = 0.15 m

`w_(x) = 1 rad/s`

`v_(By) = rw_(x) \\v_(By) = 0.15 * 1\\v_(By) = 0.15 rad/s`

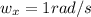
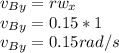
In the x - direction, r = 0.15 m,
`w_(y) = 20 rad/s`

`v_(Bx) = rw_(y) \\v_(Bx) = 0.15 * 20\\v_(Bx) = 3.0 rad/s`

`v_(B) = 3 i +0.15 j\\` m/s

Answer 2

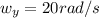
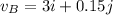Velocity between points A and B will be 0.2344 m/s