Answer:
31
Explanation:
The function given in this problem is described by the expression
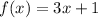
In this problem, we want to find
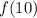
Which means that we want to evaluate the function when the value of x is 10, so when
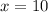
To solve the problem, we just need to substitute x = 10 into the expression of f(x). By doing so, we find:
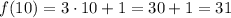
Therefore, the correct option is
31