Answer:
Therefore the radius of the can is 1.71 cm and height of the can is 2.72 cm.
Explanation:
Given that, the volume of cylindrical can with out top is 25 cm³.
Consider the height of the can be h and radius be r.
The volume of the can is V=
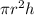
According to the problem,
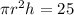
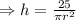
The surface area of the base of the can is =

The metal for the bottom will cost $2.00 per cm²
The metal cost for the base is =$(2.00×
 )
)
The lateral surface area of the can is =
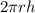
The metal for the side will cost $1.25 per cm²
The metal cost for the base is =$(1.25×
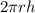 )
)
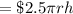
Total cost of metal is C= 2.00
 +
+

Putting
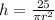
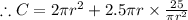
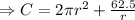
Differentiating with respect to r

Again differentiating with respect to r

To find the minimize cost, we set C'=0
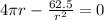

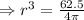
⇒r=1.71
Now,
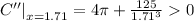
When r=1.71 cm, the metal cost will be minimum.
Therefore,
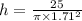
⇒h=2.72 cm
Therefore the radius of the can is 1.71 cm and height of the can is 2.72 cm.