Question

The number of accidents per week at a hazardous intersection varies with mean 2.2 and standard deviation 1.4. This distribution takes only whole-number values, so it is certainly not a normal distribution. Let "x-bar" be the mean number of accidents per week at the intersection during a year (52 weeks). What is the approximate probability that there are fewer than 100 accidents in a year? (Hint: Restate this event in terms of "x-bar")

Answer 1

The approximate probability that there are fewer than 100 accidents in a year = .9251

Explanation:

Given -

Mean
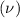`(\\u )` =2.2

Standard deviation
`\sigma` = 1.4

Let
`\overline{X}` be the mean number of accidents per week at the intersection during a year (52 weeks)

Then
`\overline{X}` =
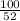`(100)/(52)` = 1.92

the approximate probability that there are fewer than 1.92 accidents per week in a year

[Z =
`\frac{\overline{X} - \\u }{(\sigma)/(√(n))}` ]

=
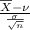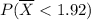`P(\overline{X} < 1.92 )` = (
`P(\frac{\overline{X} - \\u }{(\sigma)/(√(n))}< (1.92 - 2.2 )/((1.4)/(√(52))))`

= P(
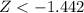`Z < -1.442` ) ( Using Z table)

= .9251