Question

A student has 67-cm-long arms. What is the minimum angular velocity (in rpm) for swinging a bucket of water in a vertical circle without spilling any? The distance from the handle to the bottom of the bucket is 35 cm .

Answer 1

29.6 rpm

Step-by-step explanation:

length of arm = 67 cm

distance of handle to the bottom = 35 cm

radius of rotation, R = 67 + 35 = 102 cm = 1.02 m

The centripetal force acting on the bucket is balanced by the weight of the bucket.

mRω² = mg

R x ω² = g

`\omega = \sqrt(g)/(R)`

`\omega = \sqrt(9.8)/(1.02)`

ω = 3.1 rad/s

Let f is the frequency in rps

ω = 2 x 3.14 x f

3.1 = 2 x 3.14 xf

f = 0.495 rps

f = 29.6 rpm

Answer 2

29.61 rpm.

Step-by-step explanation:

Given,

student arm length, l = 67 cm

distance of the bucket, r = 35 m

Minimum angular speed of the bucket so, the water not fall can be calculated by equating centrifugal force with weight.

Now,

`mg = m r \omega^2`

`\omega = \sqrt{(g)/(R)}`

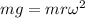
R = 67 + 35 = 102 cm = 1.02 m

`\omega = \sqrt{(9.81)/(1.02)}`

`\omega = 3.101\ rad/s`

`\omega = (3.101)/(2\pi) = 0.494\ rev/s`

`\omega = 0.494 * 60 = 29.61\ rpm`

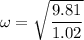
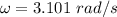
minimum angular velocity is equal to 29.61 rpm.