Question

Which expressions have a value of Negative StartFraction 1 Over 64 EndFraction? Check all that apply.

(Negative one-fourth) cubed
Negative (one-fourth) cubed
(Negative StartFraction 1 Over 8 EndFraction cubed
Negative (StartFraction 1 Over 8 EndFraction) squared
(Negative one-half) Superscript 6
Negative (one-half) Superscript 6

Answer 1

Here are the answers:

Option A: (Negative one-fourth) cubed

Option B: Negative (one-fourth) cubed

Option D: Negative (StartFraction 1 Over 8 EndFraction) squared

Option F: Negative (one-half) Superscript 6

Explanation:

Answer 2

Correct Options are:

Option A: (Negative one-fourth) cubed

Option B: Negative (one-fourth) cubed

Option D: Negative (StartFraction 1 Over 8 EndFraction) squared

Option F: Negative (one-half) Superscript 6

Explanation:

We need to check the expressions that have value
`-(1)/(64)`

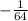
Option A: (Negative one-fourth) cubed

`(-(1)/(4))^3`

Solving:
`(-(1)/(4))^3`

We get
`-(1)/(64)`

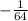
So, Option A is correct.

Option B: Negative (one-fourth) cubed

`-((1)/(4))^3`

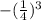
Solving:
`-((1)/(4))^3`

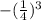
We get
`-(1)/(64)`

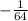
So, Option B is correct

Option C: (Negative StartFraction 1 Over 8 EndFraction cubed

`(-(1)/(8))^3`

Solving:
`(-(1)/(8))^3`

We get
`-(1)/(512)`

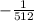
So, Option C is not correct.

Option D: Negative (StartFraction 1 Over 8 EndFraction) squared

`-((1)/(8))^2`

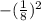
Solving:
`-((1)/(8))^2`

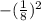
We get
`-(1)/(64)`

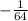
So, Option D is correct.

Option E: (Negative one-half) Superscript 6

`(-(1)/(2))^6`

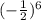
Solving:
`(-(1)/(2))^6`

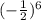
We get:
`(1)/(64)`

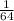
So, Option E is not correct.

Option F: Negative (one-half) Superscript 6

`-((1)/(2))^6`

Solving:
`-((1)/(2))^6`

We get:
`-(1)/(64)`

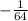
So, Option F is correct.

So, correct Options are: Option A, B, D and F