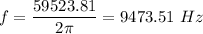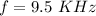Answer:
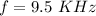
Step-by-step explanation:
AC Circuit
When connected to an AC circuit, the capacitor acts as an impedance of module
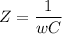
Where w is the angular frequency of the power source and C is the capacitance.
If the capacitor is the only element connected to a circuit, then the Ohm's law establishes that
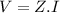
Where V and I are the rms voltage and current respectively. Replacing the value of Z, we have
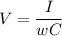
Solving for w
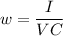
The question provides us the following values
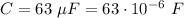
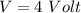
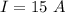
Plugging in the values
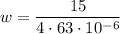
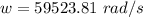
Since
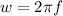
Then