Question

Can someone help me please? It’s like my 3rd time trying to get some answers for this question. Thanks. :)

Answer 1

both rates of change equal the slope of the line (3/4)

Explanation:

Part a)

We calculate the rate of change using the formula:

`(y_2-y_1)/(x_2-x_1)`

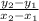
for the first interval [0,6], we calculate the y-values at x=0 and x=6;

at x=0 :
`y=(3)/(2) (0)+2=2`

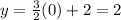
at x=6 :
`y=(3)/(2) (6)+2=11`

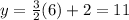
therefore, the rate of change in this interval is:
`(y_2-y_1)/(x_2-x_1)=(11-2)/(6-0)=(9)/(6) =(3)/(2)`

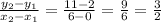
For the second interval [-4,4], we calculate the y-values at x=-4 and x=4;

at x=-4 :
`y=(3)/(2) (-4)+2=-4`

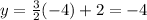
at x=4 :
`y=(3)/(2) (4)+2=8`

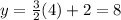
therefore, the rate of change in this interval is:
`(y_2-y_1)/(x_2-x_1)=(8-(-4))/(4-(-4))=(12)/(8) =(3)/(2)`

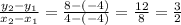
Part b):

Notice that both rates of change equal the value of the slope of the linear function (3/2)