Question

Consider a sampling distribution with p equals 0.15p=0.15 and samples of size n each. Using the appropriate​ formulas, find the mean and the standard deviation of the sampling distribution of the sample proportion. a. For a random sample of size n equals 5000n=5000. b. For a random sample of size n equals 1000n=1000. c. For a random sample of size n equals 500n=500.

Answer 1

`a.\ \mu_p=750\ \ , \sigma_p=0.005\\\\b.\ \mu_p=150\ \ , \sigma_p=0.0113\\\\c.\ \mu_p=75\ \ , \sigma_p=0.0160`

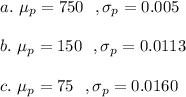
Explanation:

a. Given p=0.15.

-The mean of a sampling proportion of n=5000 is calculated as:

`\mu_p=np\\\\=0.15* 5000\\\\=750`

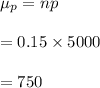
-The standard deviation is calculated using the formula:

`\sigma_p=\sqrt{(p(1-p))/(n)}\\\\=\sqrt{(0.15(1-0.15))/(5000)}\\\\=0.0050`

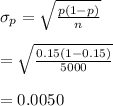
Hence, the sample mean is μ=750 and standard deviation is σ=0.0050

b. Given that p=0.15 and n=1000

#The mean of a sampling proportion of n=1000 is calculated as:

`\mu_p=np\\\\=1000* 0.15\\\\\\=150`

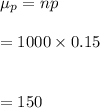
#-The standard deviation is calculated as follows:

`\sigma_p=\sqrt{(p(1-p))/(n)}\\\\\\=\sqrt{(0.15* 0.85)/(1000)}\\\\\\=0.0113`

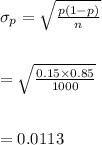
Hence, the sample mean is μ=150 and standard deviation is σ=0.0113

c. For p=0.15 and n=500

#The mean is calculated as follows:

`\mu_p=np\\\\\\=0.15* 500\\\\=75`

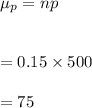
#The standard deviation of the sample proportion is calculated as:

`\sigma_p=\sqrt{(p(1-p))/(n)}\\\\\\=\sqrt{(0.15* 0.85)/(500)}\\\\\\=0.0160`

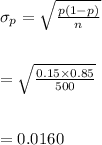
Hence, the sample mean is μ=75 and standard deviation is σ=0.0160