Question

the lateral area of a cone is 558pi cm^2 the radius is 31 cm. find the slant height to the nearest tenth

Answer 1

The slant height of the cone is 39.7 cm

Step-by-step explanation:

Given:

Lateral surface area of a cone = 558π cm²

Radius, r = 31 cm

Slant height, l = ?

We know:

`A = \pi r√(h^2+r^2)`

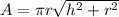
Where,

h is the height of the cone

r is the radius

Solving the equation further:

`558\pi = \pi r√(h^2+r^2) \\\\558 = 31√(h^2+(31)^2) \\\\(18)^2 = h^2 + 961\\\\324 = h^2+ 961\\\\h = 25.23`

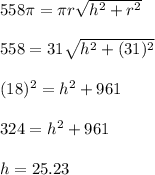
Lateral height, H = ?

Applying pythagoras theorm,

(H)² = (h)² + (r)²

(H)² = (25.23)² + (31)²

(H)² = 636.55 + 961

(H)² = 1597.55

H = 39.7 cm

Therefore, the slant height of the cone is 39.7 cm