Question

In one region of the Caribbean​ Sea, daily water temperatures are normally distributed with a mean of 77.9 degrees Fahrenheit and a standard deviation of 2.4 degrees Fahrenheit. What temperature separates the lowest​ 59.5% of temperatures from the​ rest?

Answer 1

The temperature that separates the lowest​ 59.5% of temperatures from the​ rest is 83.66 degrees Fahrenheit.

Explanation:

Mean temperature = u = 77.9

Standard Deviation =
`\sigma` = 2.4

Since the distribution is normal and we have the value of population standard deviation, we will use the concept of z-score to find the desired value.

We have to find the value that separates lowest 59.5% of the temperature from the rest. This means our desired value is above 59.5% of the data values.

From the z-table we can find a z-score which is above 59.5% of the values and then convert it to its equivalent temperature using the formula.

From the z-table, the z-score which is above 59.5% of the value is:

z = 0.24

The formula for z-score is:

`z=(x-\mu)/(\sigma)`

Using the values we have:

`0.24=(x-77.9)/(2.4)\\\\ 5.76=x-77.9\\\\ x=83.66`

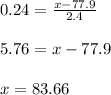
This is our data value equivalent to a z-score of 0.24. Just like 59.5% of z values were below 0.24, in the same manner, 59.5% of temperatures are below 83.66 degrees Fahrenheit.

Therefore, the temperature that separates the lowest​ 59.5% of temperatures from the​ rest is 83.66 degrees Fahrenheit.