Question

you are riding a bicycle which has tires with a 25-inch diameter at a steady 15-miles per hour, what is the angular velocity of a point outside the tire in radians per second? give your answer in terms of pi rounding the coefficient to the nearest hundredth.

Answer 1

The angular velocity is 6.72 π radians per second

Explanation:

The formula of the angular velocity is ω =
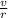`(v)/(r)` , where v is the linear velocity and r is the radius of the circle

The unit of the angular velocity is radians per second

∵ The diameter of the tire is 25 inches

∵ The linear velocity is 15 miles per hour

- We must change the mile to inch and the hour to seconds

∵ 1 mile = 63360 inches

∵ 1 hour = 3600 second

∴ 15 miles/hour = 15 ×
`(63360)/(3600)`

∴ 15 miles/hour = 264 inches per second

Now let us find the angular velocity

∵ ω =
`(v)/(r)`

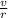
∵ v = 264 in./sec.

∵ d = 25 in.

- The radius is one-half the diameter

∴ r =
`(1)/(2)` × 25 = 12.5 in.

- Substitute the values of v and r in the formula above to find ω

∴ ω =
`(264)/(12.5)`

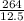
∴ ω = 21.12 rad./sec.

- Divide it by π to give the answer in terms of π

∴ ω = 6.72 π radians per second

The angular velocity is 6.72 π radians per second