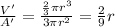Question

A storage tank will have a circular base of radius r and a height of r. The tank can be either cylindrical or hemispherical​ (half a​ sphere). Complete parts​ (a) through​ (e) below. a. Write and simplify an expression for the ratio of the volume of the hemispherical tank to its surface area​ (including the​ base). For a​ sphere, Vequals four thirds pi r cubed and SAequals 4 pi r squared . What is the volume of the hemispherical tank​ (including the​ base)? Vequals nothing ​(Simplify your answer. Type an exact answer in terms of pi ​.)

Answer 1

Volume:
`(2)/(3)\pi r^3`

Ratio:
`(2)/(9)r`

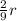
Explanation:

First of all, we need to find the volume of the hemispherical tank.

The volume of a sphere is given by:

`V=(4)/(3)\pi r^3`

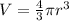
where

r is the radius of the sphere

V is the volume

Here, we have a hemispherical tank: a hemisphere is exactly a sphere cut in a half, so its volume is half that of the sphere:

`V'=(V)/(2)=((4)/(3)\pi r^3)/(2)=(2)/(3)\pi r^3`

Now we want to find the ratio between the volume of the hemisphere and its surface area.

The surface area of a sphere is

`A=4 \pi r^2`

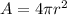
For a hemisphere, the area of the curved part of the surface is therefore half of this value, so
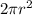`2\pi r^2`. Moreover, we have to add the surface of the base, which is
`\pi r^2`. So the total surface area of the hemispherical tank is

`A'=2\pi r^2 + \pi r^2 = 3 \pi r^2`

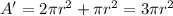
Therefore, the ratio betwen the volume and the surface area of the hemisphere is

`(V')/(A')=((2)/(3)\pi r^3)/(3\pi r^2)=(2)/(9)r`