Question

Which are characteristics of the graph of the function f(x) = (x + 1)2 + 2? Check all that apply

The domain is all real numbers,
The range is all real numbers greater than or equal to 1
The y-intercept is 3.
The graph of the function is 1 unit up and 2 units to the Daft from the graph of y = x2
The graph has two x-intercepts

Answer 1

The domain is all real numbers

The y-intercept is 3.

Explanation:

Let's analyze each statement separately. The function is

`f(x)=(x+1)^2+2`

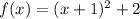
We have the following statements:

The domain is all real numbers, --> TRUE. The domain of a function is the set of values that the variable x can take. For this function, there are no restriction on the values that x can take, so the domain is all real numbers.

The range is all real numbers greater than or equal to 1 --> FALSE. The range of a function is the set of values that the variable y can take. For this function, we see that the factor
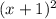`(x+1)^2` is always equal or greater than zero; this means that the minimum of the function is
`f(x)=2`, so the range is all real numbers greater than or equal to 2.

The y-intercept is 3. --> TRUE. The y-intercept is the value of the function when x = 0. For this function, if we substitute x = 0, we find:

`f(0)=(0+1)^2+2=1^2+2=3`

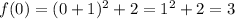
The graph of the function is 1 unit up and 2 units to the left from the graph of
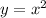`y=x^2` --> FALSE. The graph of a function is scaled n units up when
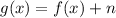`g(x)=f(x)+n`; in this case, we see that the factor n in our fuction is n = 2, so the function is actually scaled 2 units up, not 1.

The graph has two x-intercepts --> FALSE. The x-intercept of a graph is the value of x when
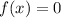`f(x)=0`. If we require
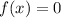`f(x)=0` for our function, we get:

`0=(x+1)^2+2\\\rightarrow (x+1)^2=-2`

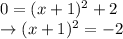
However, this equation has no solutions: so, the graph has no x-intercepts.