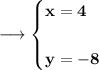Question

Three times a number plus three times a second number is negative twelve. Five times the first number plus twice the second is four

Answer 1

Consider the numbers as, if we assume our first number to be x and second number being y, then from the given information we will be having the following equations :

`{:\implies \quad \begin{cases}\sf 3x+3y=-12\\ \\ \sf 5x+2y=4\end{cases}}`

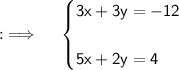
Now, rewrite the second equation as ;

`{:\implies \quad \sf 3(x+y)=-12}`

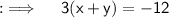
Divide both sides by 3 ;

`{:\implies \quad \sf x+y=-4\quad ---(i)}`

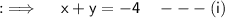
Now, consider the second equation of the above cases

`{:\implies \quad \sf 5x+2y=4\quad ---(ii)}`

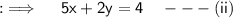
Now, multiply (i) by 2 on both sides :

`{:\implies \quad \sf 2x+2y=-8\quad ---(iii)}`

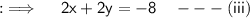
Now, subtracting (ii) from (iii) will give us :

`{:\implies \quad \sf 2x+2y-(5x+2y)=-8-4}`

`{:\implies \quad \sf 2x+2y-5x-2y=-12}`

`{:\implies \quad \sf -3x=-12}`

`{:\implies \quad \boxed{\bf{x=4}}}`

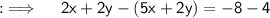
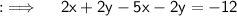
Now, putting x = 4 in (i), will give y + 4 = -4, then solving for y will yield
`{\boxed{\bf{y=-8}}}`

Hence, we can conclude that :

`{\quad \qquad \longrightarrow \begin{cases}\bf x=4\\ \\ \bf y=-8\end{cases}}`