Question

The scheduled arrival time for a daily flight from Boston to New York is 9:35 am. Historical data show that the arrival time follows the continuous uniform distribution with an early arrival time of 9:18 am and a late arrival time of 9:41 am.

After converting the time data to a minute scale, calculate the mean and the standard deviation for the distribution.

Answer 1

The mean is 11.5 minutes and the standard deviation is of 6.64 minutes

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The mean is:

`M = (a+b)/(2)`

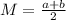
The standard deviation is:

`S = \sqrt{((b-a)^(2))/(12)}`

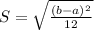
Arrival time of 9:18 am and a late arrival time of 9:41 am.

9:41 is 23 minutes from 9:18. So the time is uniformily distributed between 0 and 23 minutes, so a = 0, b = 23.

Mean:

`M = (a+b)/(2) = (0+23)/(2) = 11.5`

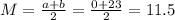
Standard deviation:

`S = \sqrt{((b-a)^(2))/(12)} = \sqrt{((23 - 0)^(2))/(12)} = 6.64`

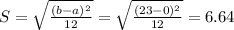
The mean is 11.5 minutes and the standard deviation is of 6.64 minutes